A curve defines a function for calculating a price calculation value. It is made up of a series of segments. A segment defines the curve's result values (y-values) within a specified range of parameter values (x-values). In addition, a curve has a default value, which defines the curve's y-value for all x-values larger than the break point of the last segment.
The first segment applies for all x-values less than or equal to its break point. The remaining segments apply for all x-values larger than the break point of the preceding segment and less than or equal to its own break point. The curve's default value applies to all x-values larger than the break point of the last segment (or for all x-values if no segments are defined).
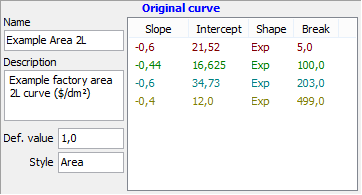
A segment has four parameters:
- slope – the slope or decay rate of the segment
- intercept – the magnitude of the segment
- shape – specifies a linear or exponential segment
- break – the largest x-value for the segment
Linear segments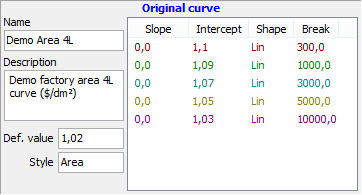
A linear segment is evaluated as follows:
y = x * slope + intercept
The intercept specifies the y-value when x=0.
The slope specifies how much the y-value changes as the x-value increases. A slope of zero means that the y-value is the same for any x-value within the range of the segment.
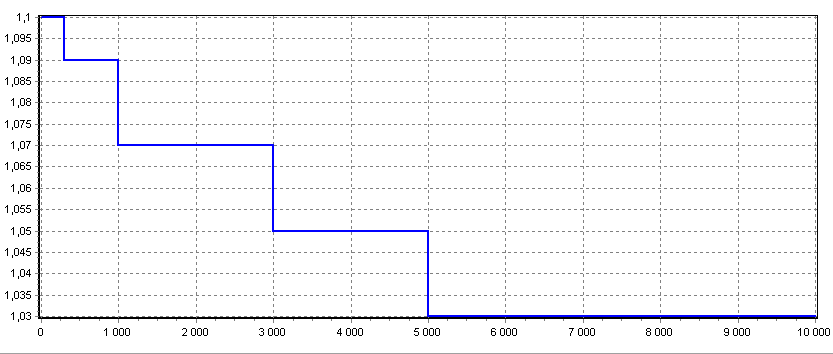
The pictures at the right show an example of an area curve using linear segments in a stairstep model. In this example the area price is $1.1/dm² for an order of up to 3m², $1.09/dm² for an order between 3m² and 10m², and so on. For orders >100m², the default value of $1.02/dm² is used.
 Exponential segments
Exponential segments
An exponential segment is evaluated as follows:
y = intercept * xslope
The intercept specifies the y-value when x=1.0.
The slope specifies the decay rate. The slope should be negative for a decay. The larger (more negative) the slope magnitude, the steeper the decay. A slope of zero gives y=intercept for any x-value within the range of the segment. A slope of -1 gives y*x=intercept for any x-value within the range of the segment.
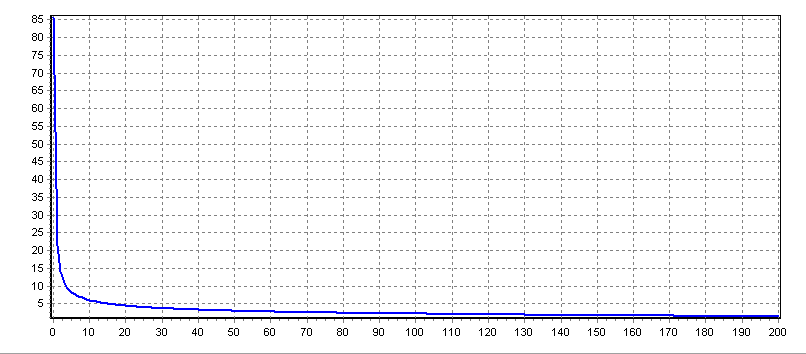
The pictures at the right show an example of an area curve using exponential decay segments. In this example, the break points are chosen to fall at the x-values where the two segments cross, in order to give a smooth overall curve.



